En retrouvant les théorèmes de Hajòs, Vuza a aussi donné un algorithme permettant de donner des cas de factorisations acycliques des «mauvais» groupes (Z/72Z, par exemple). Par construction, il donne deux ensembles dont tous les termes sont compatibles. Exemple : pour on a solutions.

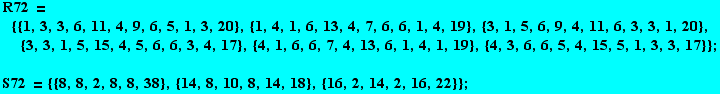
Cet algorithme, implémenté en Mathematica par Noll & Andreatta mais aussi intégré à OpenMusic (je crois par Carlos Agon) et ses résultats ont permis de donner un bon répertoire de canons rythmiques acycliques, que nous appellerons dorénavant les Vuza canons.
Il a été prouvé par Harald Fripertinger que divers procédés, observés d'ailleurs par d'autres chercheurs, permettent de fabriquer des canons acycliques que l'algorithme est incapable d'atteindre. La présente communication se concentre sur cette question.

Created by Mathematica  (January 22, 2004)