Il est actuellement inaccessible de trouver tous les canons (sans critères particuliers) de taille n=72 : les algorithmes de H. Fripertinger utilisent précisément que les solutions ont des périodes internes. Sommes-nous bien sûrs d'avoir tous les canons acycliques, disons, de taille 72 ? Ceci est peut-être accessible à des ordis puissants et judicieusement programmés. Mais pour n>72…
La recherche systématique (avec tri pour l'acyclicité) de compléments est à lancer. Elle pourrait donner des réponses même pour 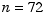, qui sait !
J'ai commencé à essayer de compléter des motifs qui pavent en période 72 avec des longueurs inédites, comme {2,4,22,2,2,2,6,4,28} (obtenu comme complément d'un motif cyclique qui pave trivialement, à savoir {1,17,1,17,1,17,1,17}) mais il y a énormément de cas et aucune garantie de trouver des canons acycliques.

Created by Mathematica  (January 22, 2004)