• n = 144=12×12 : augmentation fructueuse

    On constate que les doubles des éléments de R_72 ne figurent pas dans les Vuza-canons de période 144. C'est donc automatique de trouver des nouveaux canons, ne nous en privons pas:
    en doublant une tuile longueur 12 de période 72 et en complétant, on a trouvé
    6 * 324 = 1944 nouveaux canons acycliques !

    R72[[1]] * 2

    {2, 6, 6, 12, 22, 8, 18, 12, 10, 2, 6, 40}

    newR = complete[{2, 6, 6, 12, 22, 8, 18, 12, 10, 2, 6, 40}]

    Fait remarquable, tous sont acycliques :

    (newR = Select[newR, aperQ])//Length

    324

    All brand new Vuza! :

    newR ⋂ R144un

    newR ⋂ S144un

    vuzaQ[newR[[Random[Integer, {1, 324}]]], {2, 6, 6, 12, 22, 8, 18, 12, 10, 2, 6, 40}]

    True

    newR = Select[newR, aperQ]//Sort

    Length[newR]

    324

    Ils correspondent à un autre jeu de facteurs cyclotomiques :

    recogListe /@ newR // Union

    Intersection @@ %

    {2, 3, 6, 8, 12, 24, 48, 72}

    Il y a 10 orbites, à 12, 24 ou 48 éléments pièce :

    orbitesNewR144 = (orbite /@ newR) // Union

    orbitesNewR144//Length

    10

    Reste à chercher les compléments d'un membre de chaque orbite :

    newS144 = Union[Table[complete[orbitesNewR144[[k, 1]] ], {k, 10}]]

    newS144 = Select[Union @@ newS144, aperQ]

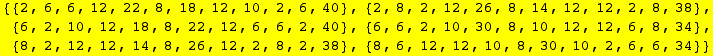
    {{2, 6, 6, 12, 22, 8, 18, 12, 10, 2, 6, 40}, {2, 8, 2, 12, 26, 8, 14, 12, 12, 2, 8, 38}, {6, 2 ... 6, 8, 34}, {8, 2, 12, 12, 14, 8, 26, 12, 2, 8, 2, 38}, {8, 6, 12, 12, 10, 8, 30, 10, 2, 6, 6, 34}}

    Ce sont des facteurs que n'a pas donné l'algorithme de Vuza,

    newS144 ⋂ S144un

    {}

    …mais ils ne sont pas nouveaux en ce sens que l'on reconnaît, comme prévu…

    In[80]:=

    R72 * 2

    Out[80]=

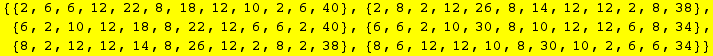
    {{2, 6, 6, 12, 22, 8, 18, 12, 10, 2, 6, 40}, {2, 8, 2, 12, 26, 8, 14, 12, 12, 2, 8, 38}, {6, 2 ... 6, 8, 34}, {8, 2, 12, 12, 14, 8, 26, 12, 2, 8, 2, 38}, {8, 6, 12, 12, 10, 8, 30, 10, 2, 6, 6, 34}}

    Created by Mathematica  (January 22, 2004)