• n = 120 : augmentations & améliorations.

    Pour commencer à partir des solutions que m'a communiqué Moreno (Vuza algo):

    In[114]:=

    orbite/@ r120//Union

    In[115]:=

    complete /@ (First /@ %)// Union

    Out[115]=

    ( 2 30 2 30 26 30 ) 8 8 14 8 8 74 ... 22 8 26 30 30 2 8 22 8 50 30 10 16 14 16 34

    Question : trouvez l'intrus !

    Essayons autre chose :
    l'augmentation de R72 par 5 donne des canons de période 240. leurs compléments sont les augmentés de S_72, rien d'intéressant là-dedans.
    Par division par 2 on obtient les facteurs acycliques suivants:

    (Dialog) In[90]:=

    {{40, 40, 10, 40, 40, 190}, {70, 40, 50, 40, 70, 90}, {80, 10, 70, 10, 80, 110}}/2

    (Dialog) Out[90]=

    {{20, 20, 5, 20, 20, 95}, {35, 20, 25, 20, 35, 45}, {40, 5, 35, 5, 40, 55}}

    Je ne sais pas trouver pour ces motifs tous les compléments acycliques (trop long à calculer…) mais avec un peu de persévérance, la méthode Monte-Carlo donne des canons inédits !!! comme les suivants:
    {1,3,3,4,8,4,7,3,1,3,23,1,6,4,12,7,3,1,3,12,11,1,3,3,4,12,7,3,4,23} ou {18,1,3,6,2,2,2,2,13,2,9,6,12,4,6,2,2,17,11,4,2,12,1,2,1,6,2,2,4,24} ou encore

    In[103]:=

    Table[randomCanonFromList[{35, 20, 25, 20, 35, 45}, 100], {10000}]//Union

    Out[101]=

    {{1, 9, 2, 1, 3, 7, 4, 4, 8, 3, 12, 6, 9, 1, 3, 10, 8, 11, 4, 11, 3, 1, 8, 1, 2, 1, 10, 1, 15, ... }, {8, 2, 4, 4, 8, 3, 3, 4, 8, 3, 13, 2, 6, 2, 8, 8, 10, 8, 15, 1, 2, 6, 2, 4, 3, 1, 8, 6, 4, 24}}

    et les membres de leurs orbites:

    In[102]:=

    Map[orbite, Drop[%, 1]] // Union

    In[104]:=

    Apply[Union, %]

    On retrouve parmi eux certains motifs Vuza:

    In[106]:=

    % ⋂ r120

    Out[106]=

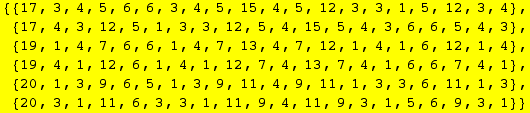
    {{17, 3, 4, 5, 6, 6, 3, 4, 5, 15, 4, 5, 12, 3, 3, 1, 5, 12, 3, 4}, {17, 4, 3, 12, 5, 1, 3, 3, ... 4, 9, 11, 1, 3, 3, 6, 11, 1, 3}, {20, 3, 1, 11, 6, 3, 3, 1, 11, 9, 4, 11, 9, 3, 1, 5, 6, 9, 3, 1}}

    Et on pourrait espérer élargir nos trouvailles en complémentant ce ce que l'on a obtenu, mais:

    In[108]:=

    complete[{16, 3, 7, 4, 2, 1, 1, 8, 1, 6, 11, 16, 10, 4, 2, 1, 9, 1, 6, 11, 4, 12, 3, 7, 4, 2, 1, 9, 1, 17}]

    Out[108]=

    {{20, 20, 5, 20, 20, 95}, {35, 20, 25, 20, 35, 45}, {40, 5, 35, 5, 40, 55}}

    Created by Mathematica  (January 22, 2004)